Red-Black Tree is a special kind of binary search tree. Each of its node is either black or red. Besides, the Red-Black tree has the following features:
- Each of its nodes is either black or red.
- The root node is black.
- Every leaf node is black. (In the Red-Black tree, the leaf node is a NIL node).
- If a node is red, its child must be black.
- From any node to its descendant leaf node must have the same number of black nodes.
The reason why we use the Red-Black tree that it’s height is always log(n), which guarantees the time complexity of its operation. The proof of Red-Black Tree’s time complexity can be found here.
An Implementation of the Red-Black tree in C++
To help understand the Red-Black tree better, implementing the Red-Black tree is a good way.
The node of the Red-Black tree
The structure of the node
First, we should consider the structure of the RB tree’s node. According to the features of the Red-Black tree, the node of Red-Black tree should contain the value, color, pointers of its child and parent. So we can get code like this:
1 | // The color of RB Tree's node. I use enum type here to make code much easier to read. |
The operation of the node
As a good programmer we should use getter and setter.
1 | template <class T> |
Good! Now the structure of RB tree is done. We can move to the next step.
RB Tree
To make the code look much tidier, I use a class to symbolize the RB tree.
1 | template <class T> |
Keep in mind that we should always record the root of the tree(For all the binary search tree), or nobody will know which node we should begin with while searching.
Rotate
Rotate is the basic operation of the binary search tree. I’ve read many books that tend to use “Left Rotate” and “Right Rotate”. In my opinion, this makes things too complex. Before looking at the following picture, I hope you know that Enum in C++ can be present as Integer. For example the RBTRelation I’ve defined before means LEFT = 0, RIGHT = 1, ERROR = 2. In the following picture, I will use Integers to present the relationship between parent and sons.(The ? means we don’t make any changes to this node. Actually, we don’t do anything to the sibling as well.).
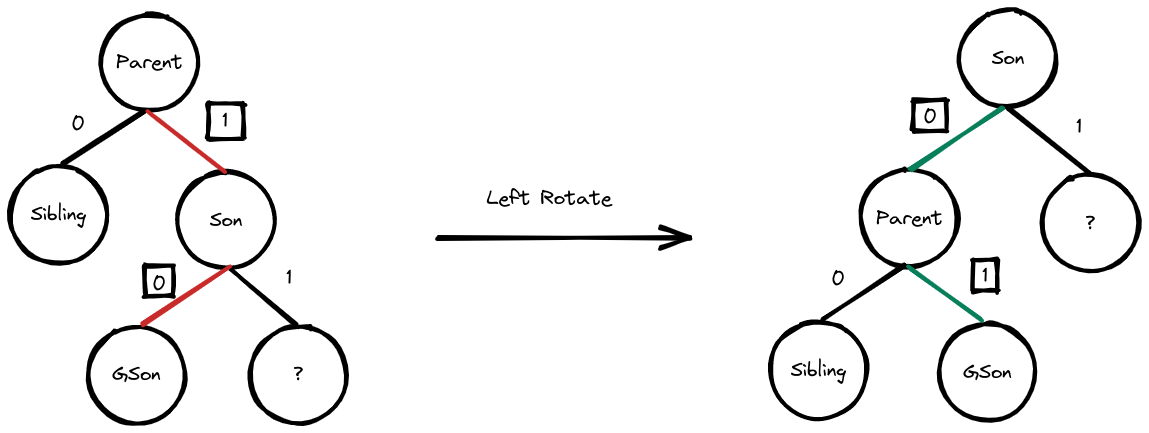
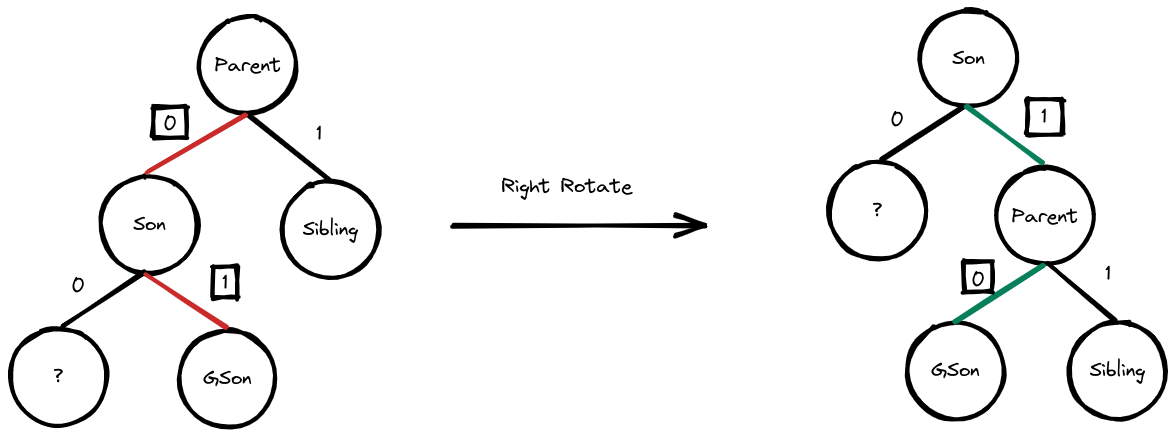
Left Rotate and Right Rotate is just like a mirror, right? What’s more, the edges between parent and sibling, son and ? never change. The edges between parent and son, son and grandson seem have a pattern. Let’s make it clear:
| Left Rotate | Right Rotate |
|---|---|
| The relation between parent and son is RIGHT(1). | The relation between parent and son is LEFT(0). |
| parent[RIGHT(1)] = son[LEFT(0)] | parent[LEFT(0)] = son[RIGHT(1)] |
| Gson->parent = parent | Gson->parent = parent |
| son->parent = grandparent | son->parent = grandparent |
| if(grandparent==NULL)root = son | if(grandparent==NULL)root = son |
| else {relation = parent->getRelation(grandparent) | else {relation = parent->getRelation(grandparent) |
| grandparent->son[relation] = son} | grandparent->son[relation] = son} |
| son->son[LEFT(0)] = parent | son->son[RIGHT(1)] = parent |
| parent->parent = son | parent->parent = son |
Almost the same, right? Even though the relationship maybe a bit different, you can correspond relationship easily. Then we can merge left rotate and right rotate into one function.
| Rotate |
|---|
| The relation between parent and son is Relationship(0,1). Define Reverse Relationship as Relationship^1 |
| parent[Relationship] = son[Reverse Relationship] |
| Gson->parent = parent |
| son->parent = grandparent |
| if(grandparent==NULL)root = son |
| else {relation = parent->getRelation(grandparent) |
| grandparent->son[relation] = son} |
| son->son[Reverse Relationship] = parent |
| parent->parent = son |
Now we can integrate left rotate and right rotate into one function-rotate! Writing two same function is a waste of life.
1 | void rotate(RBTNode<T> *&root, RBTNode<T> *node, RBTNode<T> *son){ |
Now we finish the function of ‘rotate’. At the end part of rotate, I’d like to talk about why we need rotate. Many books just tell us to remember rotate and it’s useful, but why? The reason that rotate is useful is first, after rotate, tree is still a VALID binary search tree. The relationships between each nodes are still correct. It’s impossible that after rotate a node’s left son’s value is larger than this node. This is useful while we want to balance a tree and we can adjust the height of tree without worrying about destroy the Binary search tree. Second, rotate enables us to move one node from one subtree to another, lift the current node and put down the parent node. This is useful to RB tree and some other special binary search tree like splay. In the part ‘insert’, you will see how we use rotate to move extra black nodes from one subtree to another.
Insert
Insert is a basic operation for all the binary search trees. The only difference is that RB tree need a re-balance after the insert operation. The process of insert is like this:
- Get the value of Node V.
- From the root of the tree, compare the V and the current node’s value(Begin with root). If V is smaller than the current node’s value, go to the left son of the current node. If V is bigger than the current node’s value, go to the right son of the current node. You should record current node as PARENT because we need it afterwards. Then set current node as the left son(right son). Here we suppose there is no duplicated value in an RB tree. If you want your RB tree contain duplicated value, you can add a property to the node class like “cnt” to count the times of the value. We will stop the loop when the current node is NULL.
- Set the parent of node v as PARENT.
- If PARENT is not NULL, compare the value of PARENT and the value of node. If the value of node is less than the value of PARENT, set the PARENT’s left son as node, else set the PARENT’s right son as node.
- If PARENT is NULL, set the root as PARENT.
- Set the node as RED.
- Re-balance the RB Tree.
1 | // Insert new node |
Why we choose to set the node as RED? It’s because this will break as fewer rules of the RB tree as possible. Let’s consider the rules of RB tree:
- Each of its node is either black or red. (YES, we set the new node as RED)
- The root node is black.(If at the beginning the tree is empty, we may break this rule).
- Every leaf node is black. (In RB tree, the leaf node is a NIL node). (YES, although the node we insert is RED, we set two leaf nodes as BLACK by default).
- If a node is red, its child node must be black.(NO, the node we insert is red, and its parent maybe red as well).
- From any node to its descendant leaf node must have the same number of black nodes. (YES, the node we insert is red, which won’t affect the number of black nodes. Be careful that actually we substitute a black node with the red node, that’s why the number of black nodes won’t change).
So, we should do two things in the re-balance. First, we should set the root node as black. Second, we should solve the problem that the parent node and child node can’t be both red. To solve this problem, we have to discuss different situations. Here is the first situation.
(1) Parent is red, uncle is red as well.
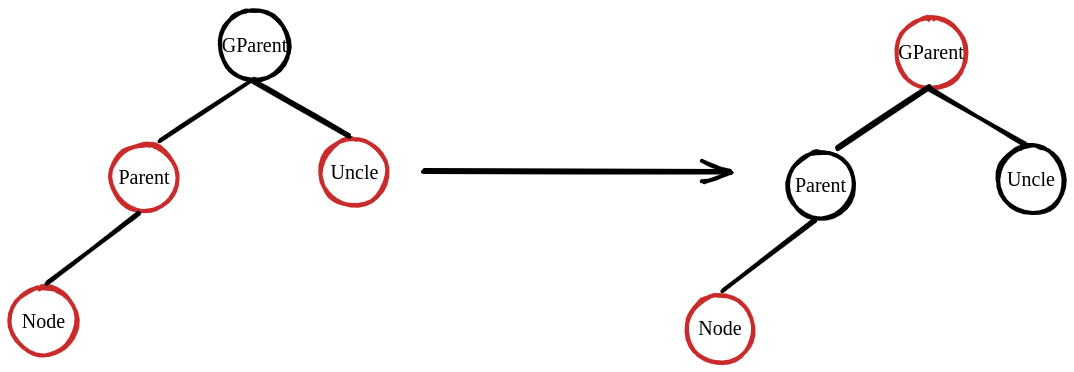
Under this situation, the first thing we can do is to change parent to Black. Good! Now we won’t break rule 4. However, this may break rule 5. The black nodes on GParent-Parent-Node plus 1, and is no longer equal to the number of black nodes on GParent-Uncle, not to mention the other part of tree. The only thing we can do is to change uncle to black, and then change GParent to Red. Now at least the sub-tree obeys the rules of RB tree. But there is still possible that GParent’s parent is red. So we need to take GParent as Node and repeat.
P.S. GParent must be black because the RB tree before we insert is valid. So it’s impossible that parent is red and GParent is red as well.
(2)Parent is Red, Uncle is Black. The relationship between GParent and Parent, Parent and Node is same.
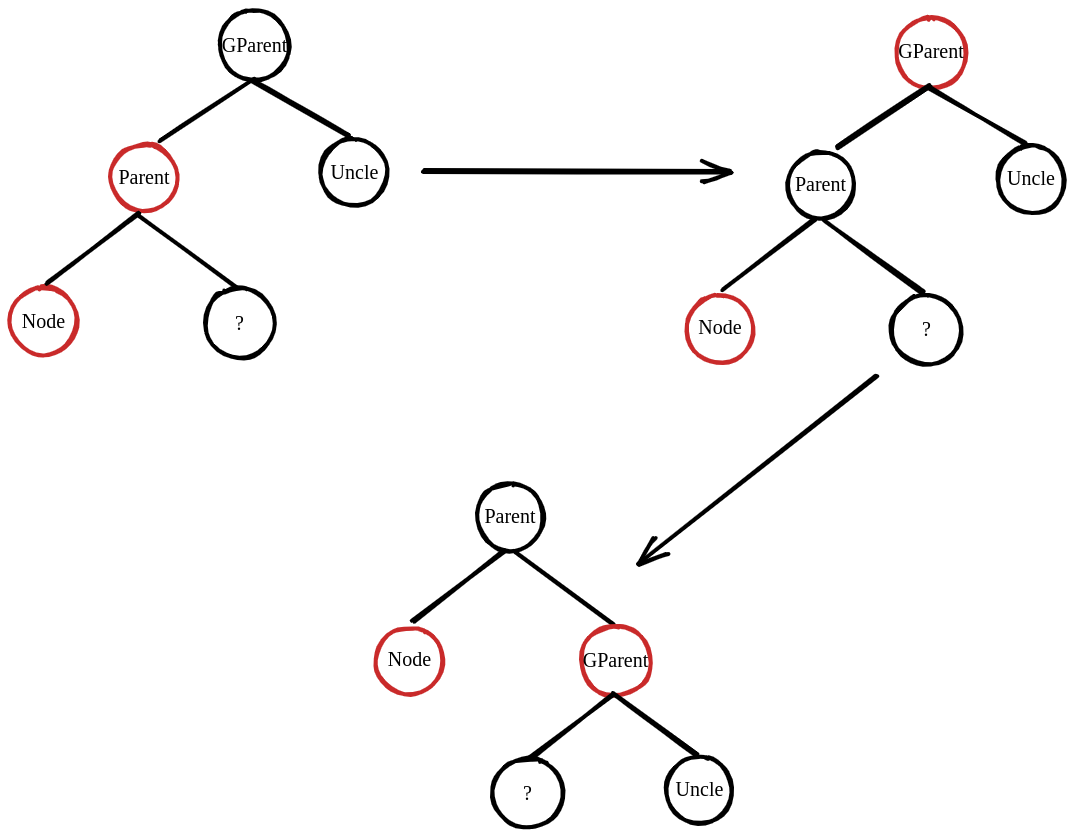
First we still change parent to black, then change GParent to red like what we did before. The RB tree seemed balance right? But actually GParent-Uncle used to have 2 black nodes, and they have only one now. We break the rule 5! The only thing we can do is to rotate parent and GParent to re-arrange the relationship of the subtree.
Does the re-balance over? No.
(3)Parent is Red, Uncle is Black. The relationship between GParent and Parent, Parent and Node is different.
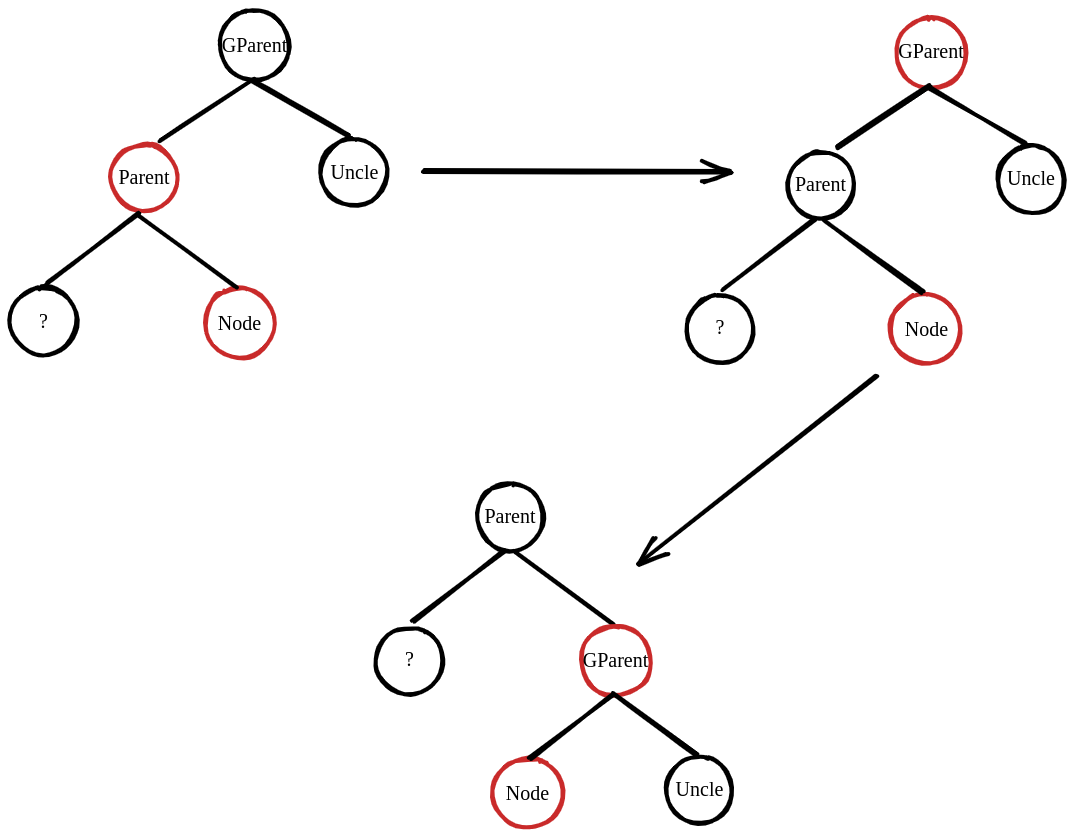
Oh! Nothing changes! It is because we make Node the GParent’s son right? So the solution is to make the node that we will rotate Black. Be careful that we can’t change the Node black. Do you remember why we set Node red before. What shall we do? Let look back at situation (2). We are lazy, and how about change situation (3) to (2)? Ya, rotate parent and node right?

Now we can solve situation (3) like situation (2)! Remember that the parent and node’s relationship is a bit different, if you use pointers to point at node and parent, you may use swap(parent, node) to ‘repair’ the pointers.
1 | void insertRebalance(RBTNode<T> *&root, RBTNode<T> *node){ |
Search
Search is a very basic operation of binary search Tree. As binary search tree has such a property that left sons’ value are smaller than the current node, the right sons’ values are larger than the current node, we can search from the root and compare the value and the current node’s value. If the value is smaller than the current node’s value, go to the left son. Else we go to the right son.
1 | RBTNode<T> *searchByValue(RBTNode<T> *cur, T val){ |
FindMin, FindMax
For a subtree, we should be able to find the minimum and maximum element of it. It’s very easy because we just need to search the tree along the left/right node we will find the min/max value of the subtree.
1 | // Find the node with minimum value. |
Successor, Predecessor
The successor is the smallest node whose value is larger than the current node. The predecessor is the largest node whose value is smaller than the current node. Here I will explain how to get the successor, and you can get predecessor in almost the same way. If a node has right son node, then the minimum node in the right son’s subtree is the successor. If the node doesn’t have right son, we need to check the node’s parent. If the node is the left son of the parent, then the parent is the successor. If the node is the right son of the parent, we need to find the parent of the parent, until we find a node is the left son of its parent. Then the parent is the successor.
1 | RBTNode<T> *successor(RBTNode<T> *node){ |
Delete
The delete operation is very similar to the delete operation in Binary search tree. We should first find out the node with the value we want to delete, then we should consider the following situation:
- The node to be deleted is a leaf node. (We can delete it without extra operation).
- The node to be deleted has only one son. (We can replace the node with its son, keep in mind that we won’t change the color).
- The node to be deleted has two sons. (We need to find out the successor of the node, then replace the node with its successor. Finally we can delete the successor. The successor must have no or only one child as it’s the successor of current node. So it fall into situation 1 or 2).
1 | void removeByVal(RBTNode<T> *&root, RBTNode<T> *node){ |
After delete, of course, we need to re-balance the tree. Fortunately, as we delete the successor node, we can make sure that this is a leaf node, which means we don’t need to both re-balance the tree from the node to the root and from the node to the leaf. Great! Now let see we have broken which rules of RB tree:
- Each of its nodes is either black or red. (YES)
- The root node is black. (NO, do you remember that we need to replace the root with the successor node?)
- Every leaf node is black. (In the Red-Black tree, the leaf node is a NIL node).(YES)
- If a node is red, its child node must be black. (NO, if there is one son, the parent maybe red and the son is red as well).
- From any node to its descendant leaf node must have the same number of black nodes. (NO, the same reason as rule 2)
Now we know the conflict we need to solve is 2, 4, 5.
For rule 2, we can simply set the root as black to solve it.
For rule 4, the only question is that for the node we want to delete, its parent and its only son may be both red. OK, after replace the node with its only son, just set it black. (Node is black, so we won’t break rule 5 as well!)
So, only question is 5 and only if the node has two sons! Now the question become how to re-balance the successor. If the successor is red, perfect! Delete it won’t break the rule 5. If the successor is black, we need to “add” a black node to the path from the root to the successor node. We can’t insert a node so the only way is to rotate.
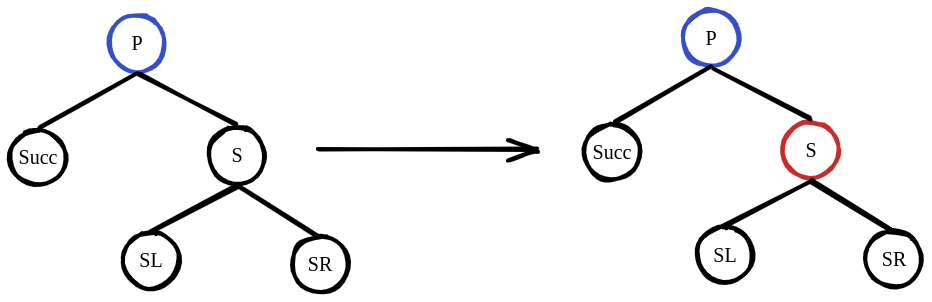
(1) Successor is Black, Sibling is Black, Sibling’s right son is Red

For such condition, left rotate can make the black nodes on the path from root to successor plus 1. Be careful that it’s possible that P is red and SL is red as well. So we need to set P as Black, but this may cause the number of black nodes change. So the best solution is to swap the color of P and S. Now we need to check rules 5 after the left rotate:
I. The black nodes on the path from root to successor remain the same.
Yes, the S node helps us solve the problem. Now we can delete the successor.
II. The black nodes on the path from root to SL remain the same.
As we swap the color of S and P, so this won’t be a problem.
III. The black nodes on the path from the root to SR remain the same.
As the left node minus 1, we need to change SR into Black.
Now I think you know why we emphasize that SR must be red. When we change a red node into black, we will only break rule 5, and by chance we need to add a black node on this path! As a result, the procedure is:
Swap the color of parent and sibling.
Set the right son of sibling as black.
Rotate(parent, sibling).
The tree is balanced!
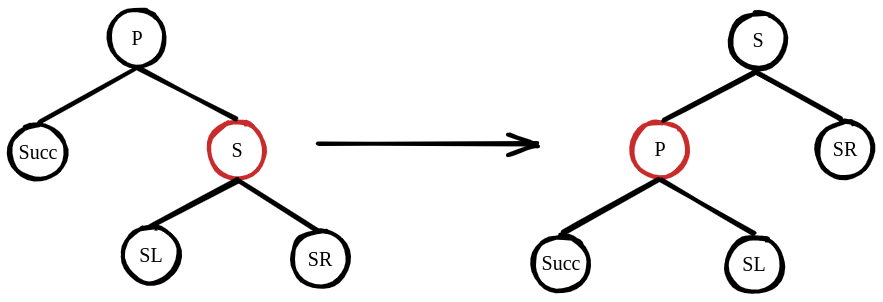
(2) Successor is Black, Sibling is Black, Sibling’s left son is Red, Sibling’s right son is Black.

This situation is very similar to (1). A right rotate on(S, SR) , then set SL as black, S as red can change (2) to (1).
- Set SL as Black.
- Set S as Red.
- Rotate(S, SR).
- Reset sibling of succ.
(3) Successor is Black, Sibling is Black, both of Sibling’s sons are Black.
Here the only thing we can do is to set S as red. Why? We all know that we need to add a black node to the path of successor, but we can do nothing here. So we will solve the problem at the parent. But keep in mind that if we do so, the path from the root to S will have an extra black node! As a result, we need to set S as red.
(4) Successor is Black, Sibling is Red
In situation 1,2 and 3, the sibling node is always black. If we find the sibling node is red, we need to change it into 1,2 and 3. We just need to set sibling as black, set parent as red and rotate(parent, sibling).
OK! Now the re-balance of delete is done! Here is the code.
1 | void removeRebalance(RBTNode<T> *node, RBTNode<T> *parent){ |
OK! Now the RB tree is done. Enjoy it.
Full Version of Code in C++
Annotation may be a bit different from the code before.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
using namespace std;
const int DEBUG = 1;
enum RBTNodeColor
{
RED,
BLACK
};
enum RBTRelation
{
LEFT,
RIGHT,
ERROR
};
// class T should override the operator <,>,==
template <class T>
class RBTNode
{
private:
T value;
RBTNodeColor color;
RBTNode<T> *child[2], *parent;
public:
RBTNode(T value, RBTNodeColor color = BLACK, RBTNode<T> *left = NULL, RBTNode<T> *right = NULL, RBTNode<T> *parent = NULL) : value(value), color(color), parent(parent)
{
child[0] = left, child[1] = right;
}
RBTNode<T> *getSon(RBTRelation relation)
{
return this->child[relation];
}
void setSon(RBTNode<T> *node, RBTRelation relation)
{
this->child[relation] = node;
}
RBTNode<T> *getParent()
{
return this->parent;
}
void setParent(RBTNode<T> *parent)
{
this->parent = parent;
}
RBTNodeColor getRBTNodeColor()
{
return this->color;
}
void setRBTNodeColor(RBTNodeColor color)
{
this->color = color;
}
RBTRelation getRelation(RBTNode *parent)
{
if (parent->getSon(LEFT) == this)
return LEFT;
else if (parent->getSon(RIGHT) == this)
return RIGHT;
else
return ERROR;
}
T getValue()
{
return this->value;
}
void setValue(T value)
{
this->value = value;
}
};
// This RBTree doesn't allow duplicated elements.
template <class T>
class RBTree
{
private:
RBTNode<T> *root;
void rotate(RBTNode<T> *&root, RBTNode<T> *node, RBTNode<T> *son)
{
if (DEBUG)
printf("Rotate Start\n");
/* Initialization:
* parent
* / (ATTENTION: Maybe left son or right son.)
* node
* / \
* leftSon son
* / \
* grandSon ?
*/
RBTNode<T> *parent = node->getParent();
RBTRelation relation = son->getRelation(node);
RBTRelation oppRelation = static_cast<RBTRelation>(1 - relation);
RBTNode<T> *grandSon = son->getSon(oppRelation);
node->setSon(grandSon, relation);
if (grandSon != NULL)
{
grandSon->setParent(node);
}
/* After the steps before, grandSon is settled.
* parent
* /
* node <=parent son
* / \ / \
* leftSon grandSon ?
*/
son->setParent(parent);
if (parent == NULL)
{
root = son;
}
else
{
RBTRelation rRelation = node->getRelation(parent);
if (rRelation == ERROR)
{
printf("ERROR: These two nodes are not parent and son.\n");
}
else
{
parent->setSon(son, rRelation);
}
}
/*
* parent
* /
* son
* / \
* node ?
* / \
* leftSon grandSon
*/
son->setSon(node, oppRelation);
node->setParent(son);
if (DEBUG)
printf("Rotate end\n");
}
// Insert new node
void insertNode(RBTNode<T> *&root, RBTNode<T> *node)
{
printf("Insert starts\n");
RBTNode<T> *parent = NULL;
RBTNode<T> *cur = root;
// Here we want to find the node where we want to insert.
while (cur)
{
parent = cur;
// Left child's value is less than the parent node, right child's value is larger than the parent node.
if (node->getValue() < cur->getValue())
cur = cur->getSon(LEFT);
else
cur = cur->getSon(RIGHT);
}
// Here we know the position to insert and also know the parent of the node.
node->setParent(parent);
if (parent != NULL)
{
if (node->getValue() < parent->getValue())
{
parent->setSon(node, LEFT);
}
else
{
parent->setSon(node, RIGHT);
}
}
// Don't forget the condition that the RBtree is NULL.
else
{
root = node;
}
/* When we are inserting a new node, we should always set it RED.
* Considering the rules of RBTree:
* 1. Each of its node is either black or red.(√. We won't break it)
* 2. The root node is always black.(×.If the tree isn't NULL, the insert operation won't affect the root node.
* If the tree is NULL, the root is RED. So we need to fix it in the rebalance operation)
* 3. Every leaf node is black.(√. We won't break it)
* 4. If a node is red, its child node must be black.(×. If the parent node is red, we may break this rule)
* 5. From any node to its descendant leaf node must have the same number of black nodes.
* (√. The node we insert is red, this operation won't make the number of black nodes change)
*/
node->setRBTNodeColor(RED);
insertRebalance(root, node);
printf("Insert ends\n");
};
void insertRebalance(RBTNode<T> *&root, RBTNode<T> *node)
{
RBTNode<T> *parent, *grandParent;
while ((parent = node->getParent()) && parent->getRBTNodeColor() == RED)
{
grandParent = parent->getParent();
RBTNode<T> *uncle = grandParent->getSon(static_cast<RBTRelation>(1 - parent->getRelation(grandParent)));
if (uncle && uncle->getRBTNodeColor() == RED)
{
uncle->setRBTNodeColor(BLACK);
parent->setRBTNodeColor(BLACK);
grandParent->setRBTNodeColor(RED);
node = grandParent;
}
else if (uncle == NULL || uncle->getRBTNodeColor() == BLACK)
{
RBTRelation gPRelation = parent->getRelation(grandParent);
RBTRelation pSRelation = node->getRelation(parent);
if (gPRelation != pSRelation)
{
rotate(root, parent, node);
swap(parent, node);
}
parent->setRBTNodeColor(BLACK);
grandParent->setRBTNodeColor(RED);
rotate(root, grandParent, parent);
}
}
root->setRBTNodeColor(BLACK);
};
// Find the node with minimum value.
RBTNode<T> *findMin(RBTNode<T> *node)
{
RBTNode<T> *cur = node;
while (cur->getSon(LEFT) != NULL)
{
cur = cur->getSon(LEFT);
}
return cur;
}
// Find the node with maximum value.
RBTNode<T> *findMax(RBTNode<T> *node)
{
RBTNode<T> *cur = node;
while (cur->getSon(RIGHT) != NULL)
{
cur = cur->getSon(RIGHT);
}
return cur;
}
RBTNode<T> *successor(RBTNode<T> *node)
{
if (node->getSon(RIGHT) != NULL)
{
return findMin(node->getSon(RIGHT));
}
RBTNode<T> *nxt = node->getParent();
RBTNode<T> *cur = node;
while ((nxt != NULL) && (cur == nxt->getSon(LEFT)))
{
cur = nxt;
nxt = nxt->getParent();
}
return cur;
}
RBTNode<T> *predecessor(RBTNode<T> *node)
{
if (node->getSon(LEFT) != NULL)
{
return findMax(node->getSon(LEFT));
}
RBTNode<T> *nxt = node->getParent();
RBTNode<T> *cur = node;
while ((nxt != NULL) && (cur == nxt->getSon(RIGHT)))
{
cur = nxt;
nxt = nxt->getParent();
}
return cur;
}
RBTNode<T> *searchByValue(RBTNode<T> *cur, T val)
{
if (!cur || cur->getValue() == val)
{
return cur;
}
if (val < cur->getValue())
{
return searchByValue(cur->getSon(LEFT), val);
}
else
{
return searchByValue(cur->getSon(RIGHT), val);
}
}
void removeByVal(RBTNode<T> *&root, RBTNode<T> *node)
{
// If node's left and right are both not NULL.
printf("Remove starts\n");
if ((node->getSon(LEFT) != NULL) && (node->getSon(RIGHT) != NULL))
{
printf("Situation of node has two sons.\n");
RBTNode<T> *replace = successor(node);
cout << "Successor is:" << replace->getValue() << endl;
RBTNode<T> *parent = node->getParent();
if (parent)
{
if (parent->getSon(LEFT) == node)
{
parent->setSon(replace, LEFT);
}
else
{
parent->setSon(replace, RIGHT);
}
}
else
{
root = replace;
}
RBTNode<T> *succChild = replace->getSon(RIGHT);
RBTNode<T> *succParent = replace->getParent();
RBTNodeColor color = replace->getRBTNodeColor();
if (succParent == node)
{
succParent = replace;
}
else
{
if (succChild)
succChild->setParent(succParent);
succParent->setSon(succChild, LEFT);
replace->setSon(node->getSon(RIGHT), RIGHT);
node->getSon(RIGHT)->setParent(replace);
}
replace->setParent(node->getParent());
replace->setRBTNodeColor(node->getRBTNodeColor());
replace->setSon(node->getSon(LEFT), LEFT);
node->getSon(LEFT)->setParent(replace);
if (color == BLACK)
{
removeRebalance(succChild, succParent);
}
delete node;
return;
}
RBTNode<T> *child, *parent;
RBTNodeColor color;
if (node->getSon(LEFT) != NULL)
child = node->getSon(LEFT);
else
child = node->getSon(RIGHT);
parent = node->getParent();
color = node->getRBTNodeColor();
if (child)
{
child->setParent(parent);
}
if (parent)
{
if (parent->getSon(LEFT) == node)
{
parent->setSon(child, LEFT);
}
else
{
parent->setSon(child, RIGHT);
}
}
else
{
root = child;
}
if (color == BLACK)
{
removeRebalance(child, parent);
}
delete node;
}
void removeRebalance(RBTNode<T> *node, RBTNode<T> *parent)
{
printf("removeRebalance starts\n");
RBTNode<T> *sibling;
while ((!node || node->getRBTNodeColor()) == BLACK && node != root)
{
RBTRelation relation = node->getRelation(parent);
RBTRelation oppRelation = static_cast<RBTRelation>(1 - relation);
sibling = parent->getSon(oppRelation);
// Case.4 If sibling is red
if (sibling->getRBTNodeColor() == RED)
{
sibling->setRBTNodeColor(BLACK);
parent->setRBTNodeColor(RED);
rotate(root, parent, sibling);
}
// Case.3 If sibling is black, the two sons of sibling is black as well.
if ((!sibling->getSon(LEFT) || sibling->getSon(LEFT)->getRBTNodeColor() == BLACK) &&
(!sibling->getSon(RIGHT) || sibling->getSon(RIGHT)->getRBTNodeColor() == BLACK))
{
sibling->setRBTNodeColor(RED);
node = parent;
parent = node->getParent();
}
else
{
if (!sibling->getSon(oppRelation) || sibling->getSon(oppRelation)->getRBTNodeColor() == BLACK)
{
sibling->getSon(relation)->setRBTNodeColor(BLACK);
sibling->setRBTNodeColor(RED);
rotate(root, sibling, sibling->getSon(relation));
sibling = parent->getSon(oppRelation);
}
else
{
sibling->setRBTNodeColor(parent->getRBTNodeColor());
parent->setRBTNodeColor(BLACK);
sibling->getSon(oppRelation)->setRBTNodeColor(BLACK);
rotate(root, parent, sibling);
node = root;
break;
}
}
}
if (node)
node->setRBTNodeColor(BLACK);
printf("removeRebalance ends\n");
}
public:
// Construction Function
RBTree()
{
root = NULL;
}
// insert Key into RBTree
void insert(T value)
{
RBTNode<T> *newNode = NULL;
if ((newNode = new RBTNode<T>(value)) == NULL)
printf("Create Node Failed\n");
else
insertNode(this->root, newNode);
}
void print()
{
RBTNode<T> *cur = root;
cout << preOrder(cur) << endl;
}
string preOrder(RBTNode<T> *cur)
{
if (cur == NULL)
return "";
string ret = "(";
ret += to_string(cur->getValue());
if (cur->getRBTNodeColor() == RED)
ret += " RED";
else
ret += " BLACK";
if (cur->getSon(LEFT) != NULL)
ret = ret + "LEFT:" + preOrder(cur->getSon(LEFT));
if (cur->getSon(RIGHT) != NULL)
ret = ret + "RIGHT:" + preOrder(cur->getSon(RIGHT));
ret += ")";
return ret;
}
RBTNode<T> *search(T val)
{
return searchByValue(root, val);
}
void remove(T value)
{
RBTNode<T> *node;
if ((node = search(value)) != NULL)
{
removeByVal(root, node);
}
else
{
printf("Can't find the value in the RB tree!\n");
}
}
};
int main()
{
// Test our rb Tree here!
RBTree<int> rbTree;
int oper, value;
while (cin >> oper)
{
switch (oper)
{
// Test insert
case 1:
cin >> value;
rbTree.insert(value);
break;
// Test delete
case 2:
cin >> value;
rbTree.remove(value);
break;
// Test find
case 3:
{
cin >> value;
RBTNode<int> *node = rbTree.search(value);
break;
}
// Print tree in preorder.
case 4:
printf("------------------\n");
printf("Print RBTree begin\n");
rbTree.print();
printf("Print RBTree end\n");
printf("------------------\n");
break;
default:
printf("Oops, operation can't be recognized.\n");
};
}
return 0;
}
Test Cases
1 | 1 10 |
Reference
The red-black tree: Introduction and algorithm
The red-black tree: Implement of C++
Introduction of Algorithm(The third edition)
Deletion From a Red-Black Tree
Red Black Tree in DSA Thanks for Sandeep Mishra’s Contribution!